Elektronický vzdelávací materiál

Tetivové a dotyčnicové štvoruholníky

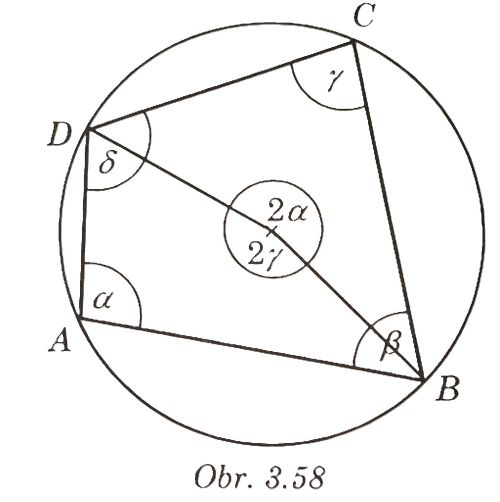
Konvexný štvoruholník, ktorému možno opísať kružnicu, sa nazýva tetivový (jeho strany sú tetivami kružnice - obr. 3.58).

Stred kružnice opísanej tetivovému štvoruholníku je v priesečníku osí strán.

Veta 3.20. Ak je štvoruholník tetivový, tak súčet veľkostí jeho pro-tiľahlých uhlov je 180°.

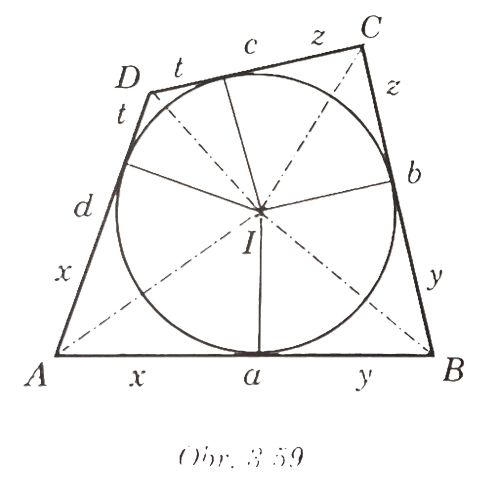
Konvexný štvoruholník, ktorému možno vpísať kružnicu, sa nazý-va dotyčnicový (jeho strany sú dotyčnicami kružnice - obr. 3.59).

Stred kružnice vpísanej dotyčnicovému štvoruholníku je v prieseč-níku osí vnútorných uhlov.

Ak je štvoruholník dotyčnicový, tak súčet veľkostí pro-tiľahlých strán je rovnaký, teda

a + c = b + d.